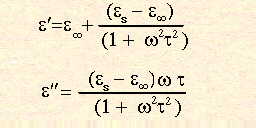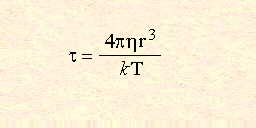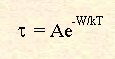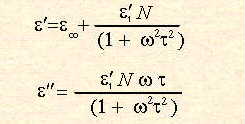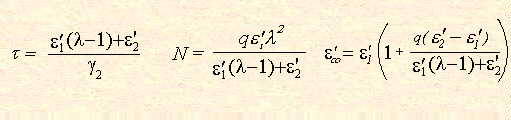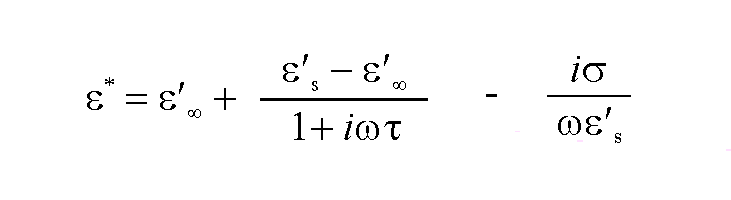|
|
 |
||||||||||||||||||||||||||||||||||||
|
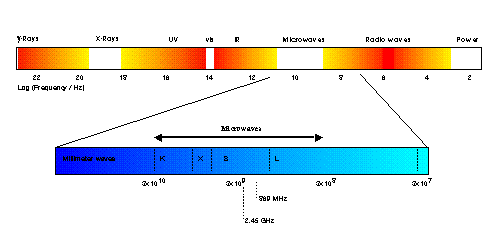
Microwave Heating Mechanisms© G. Whittaker, 1994 & 2007. This work, or extracts from this work, may be reproduced only with the written permission of the author. This version is derived from an award-winning paper first published in the Journal of Microwave Power and Electromagnetic Energy. Contents Introduction Microwaves lie in the region of the electromagnetic spectrum between millimetre waves and radio waves. Specifically, they are defined as those waves with wavelengths of between 0.01 and 1 metre, corresponding to frequencies of between 30 and 0.3GHz (Figure 1).
Figure 1 The electromagnetic spectrum
Microwave RADAR equipment operates at the lower wavelengths (0.01 - 0.25 m) of this band, and much of the band is used for telecommunications. In order to avoid interference with these uses, the wavelengths at which industrial and domestic microwave apparatus may operate is regulated at both national and international levels. In the majority of countries, 2.450 (+/- 0.050) GHz is the major operating frequency for this purpose, although other frequency allocations exist (Table 1). Where apparatus is built to operate outside these bands, efficient shielding must be used to prevent radiation leakage. All domestic ovens operate at 2.45GHz, and their popularity in recent years has resulted in progressively cheaper microwave sources at this frequency.
Table 1 Permitted Frequencies for Industrial, Medical and Scientific uses
It has long been known that materials may be heated with the use of high frequency electromagnetic waves.1 The heating effect arises from the interaction of the electric field component of the wave with charged particles in the material. Two major effects are responsible for the heating which results from this interaction. If the charged particles are free to travel through the material (electrons in a sample of carbon, for example), a current will be induced which will travel in phase with the field. If, on the other hand, the charged particles are bound within regions of the material, the electric field component will cause them to move until opposing forces balance the electric force. The result is a dipolar polarisation in the material. Conduction and dipolar polarisation may both give rise to heating under microwave irradiation, and are discussed in more detail below. It is important to note that microwave heating is quite distinct from microwave spectroscopy. The latter is a quantum phenomenon in which photons of particular energies (and therefore frequencies) excite the rotation levels of gas phase molecules. Whilst the absorption of microwaves in solid and liquid samples is frequency dependent, it is by no means quantised and does not depend upon the direct absorption of microwave photons. Rather, the material behaves as though reacting to a high frequency electric field, and so may be subjected to classical analysis.2-6 Details of this analysis are beyond the scope of this introduction, although some of its chemically significant aspects will be introduced and discussed in the following sections.
The inability of partially bound charges to follow the rapid changes in a high frequency electric field gives rise to one mechanism of microwave heating. The total polarisation (at) of the material arising from the displacement of charges may be expressed as the sum of a number of components
at = ae +aa + ad + ai
Where ae results from the displacement of electron charges in relation to the nuclei in a material, andaa from the displacement of nuclei relative to one another in materials with unequal charge distributions. Polarisation of bothae and aa operates on timescales which are very much smaller than that required for microwave frequency field reversals, and therefore follow microwave frequency fields almost exactly. As such they do not contribute to the microwave heating effect. ad results from the reorientation of polar molecules or other permanent dipoles in the material. As the timescale for its operation is of the order of those associated with microwaves, this is the most important of the polarisation phenomena in relation to microwave heating, and is discussed in some detail below. The role of the interfacial polarisation (Maxwell - Wagner) effect ai, which results from interfacial phenomena in inhomogeneous materials is limited at microwave frequencies, and in general its contribution is limited. In those cases where it is thought to be important, theoretical studies are impossible due to the large number of variables involved. The complex dielectric constant,
The real part of A further quantity, the loss angle d, is also commonly used in the literature, and is more usually given in the form of its tangent. It is related to the complex dielectric constant by;
Tan
The angle d is the phase difference between the electric field and the polarisation of the material. Magnetic polarisation may also contribute to the heating effect observed in materials where magnetic properties exist, and a similar expressions for the complex permeability of such materials may be formulated. Although such cases are relatively uncommon, a familiar example of its importance is in the microwave heating of Fe3O4.
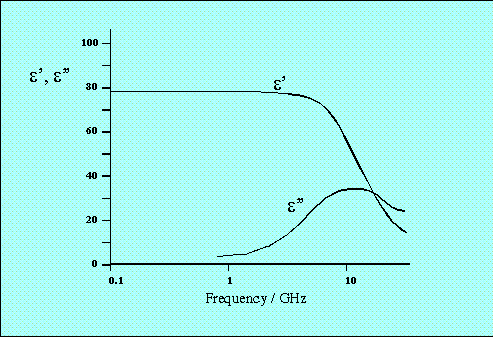
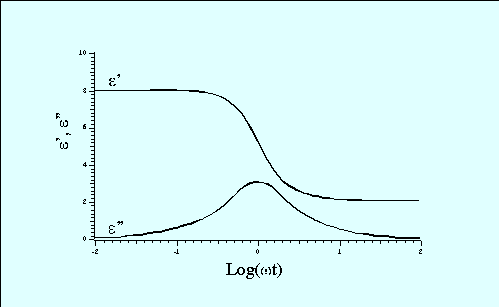
Dipolar polarisation is the phenomenon responsible for the majority of microwave heating effects observed in solvent systems. In substances such as water, the different electronegativites of individual atoms results in the existence of a permanent electric dipole on the molecule. The dipole is sensitive to external electric fields, and will attempt to align with them by rotation, the energy for this rotation being provided by the field. This realignment is rapid for a free molecule, but in liquids instantaneous alignment is prohibited by the presence of other molecules. A limit is therefore placed on the ability of the dipole to respond to a field, which affects the behaviour of the molecule with different frequencies of electric field. Under low frequency irradiation, the dipole may react by aligning itself in phase with the electric field. Whilst some energy is gained by the molecule by this behaviour, and some is also lost in collisions, the overall heating effect is small. Under the influence of a high frequency electric field, on the other hand, the dipoles do not have sufficient time to respond to the field, and so do not rotate. As no motion is induced in the molecules, no energy transfer takes place, and therefore, no heating. Between these two extremes, at frequencies which are approximately those of the response times of the dipoles, is the microwave region. The microwave frequency is low enough that the dipoles have time to respond to the alternating field, and therefore to rotate, but high enough that the rotation does not precisely follow the field. As the dipole reorientates to align itself with the field, the field is already changing, and a phase difference exists between the orientation of the field and that of the dipole. This phase difference causes energy to be lost from the dipole in random collisions, and to give rise to dielectric heating. For any material, both the real and complex dielectric constants will vary with frequency. The variation of
Figure 2 Variation of
The range of frequencies over which the dielectric loss is non-zero, indicating that microwave absorption occurs, is relatively large. This is in contrast to the linewidths of quantum spectroscopic absorption, which are typically of the order of nanometres. There is a clear maximum in the dielectric loss for water at a frequency of approximately 20GHz, the same point at which the dielectric constant In his theoretical expressions for
where
Where r is the molecular radius,
Figure 3. Debye expressions for
In solids, the molecular dipoles are no longer free to rotate as they are in liquids, but are restricted to a number of equilibrium positions, separated by potential barriers. Theoretical treatments of this behaviour have been formulated and are similar to those developed for liquids. The simplest model for this behaviour assumes that there are two potential wells separated by a potential barrier of energy W. This represents the two possible orientations of the dipole. Through statistical mechanics, it is found that the relaxation time is related to the potential barrier by;
Where A is a temperature dependent constant. In fact, most dipolar solids exhibit extremely small dielectric losses since W tends to be extremely large. Water-free ice, for example does not heat significantly under microwave irradiation.
Maxwell - Wagner (Interfacial) polarisation Where a dielectric material is not homogeneous, but consist of inclusions of one dielectric in another, it is still possible to treat the material theoretically. If the dielectric properties and geometry of the inclusions are known, it is possible to arrive at expressions for the dielectric behaviour of the bulk sample. The reverse problem - that of determining the dielectric properties of the components from that of the system - is generally insoluble except in the simplest of cases. The most basic geometrical situation was considered by Maxwell.9 This consisted of a plate capacitor of n dielectric sheets of dielectric properties and conductivities By considering small spheres with material properties
Where
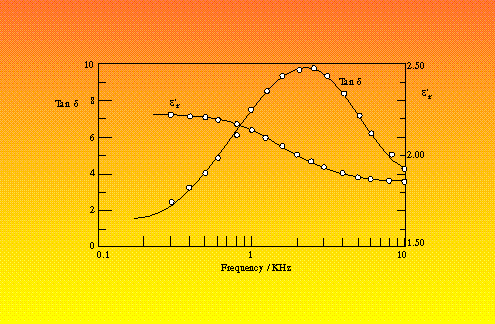
Sillars includes the dimensionless quantity, q, which is a function of the ratio a/b. The non-linear variation of this quantity implies that little can be deduced about the dielectric properties of a heterogeneous material unless the shapes of the inclusions are known. Agreement of the theoretical models with real systems has been demonstrated by the inclusion of 3% copper phthalocyanine in paraffin wax.12 At higher concentrations, account must be made of interparticle electrostatic interactions and attempts to do this have shown reasonable agreement with up to 30% water droplets in woolwax .13 and with 27.5% nitrobenzene in polystyrene 14 (Figure 4).
Figure 4 Dielectric properties of 27.5% volume nitrobenzene in polystyrene (Upper curve of each pair are experimental measurements, lower curve is the theoretical values)14
In addition to the dielectric losses describe above, many materials may also shown losses through conduction under microwave irradiation. The complex dielectric constant may be expressed to take account of these losses by including a separate conduction term :
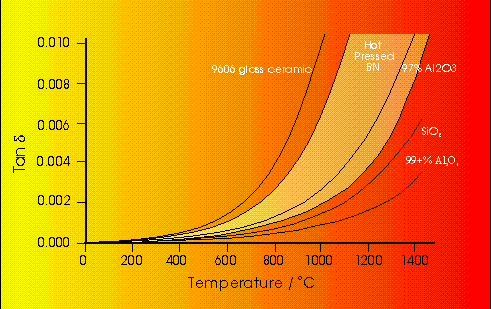
The importance of this term is displayed by a large number of systems. The addition of dissolved salts in water markedly affects the dielectric properties as conduction increases, and may become important enough to swamp the dielectric losses. On the other hand, the dielectric losses of the majority of solids arise predominantly from these conduction terms, and may be strongly affected by temperature. The conductivity of alumina, for example, increases with temperature as electrons are promoted into the conduction band from the O(2p) valence band leading to increases in the dielectric constants. This is illustrated in Figure 5 along with a number of other ceramic materials which exhibit similar behaviour.15
Figure 5 Temperature dependence of Tan[delta] for a range of ceramics 15
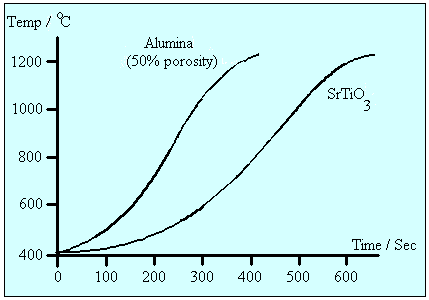
The increase in the dielectric properties with temperature is especially important in the microwave heating of solids, as it introduces the phenomenon of thermal runaway. Microwave heating in alumina is poor at room temperature, and dT/dt is therefore small. As the temperature increases so too does the dielectric loss factor and heating becomes more effective.16,17 and dT/dt increases rapidly, as illustrated for strontium titanate and alumina in Figure 6. Without careful monitoring of these materials under microwave irradiation, their temperature may rise to undesirably high levels.
Figure 6 Thermal runaway in materials under microwave irradiation16
Heating in metals and metal powders depends heavily upon conduction losses, and the important aspects of this phenomenon is treated in greater depth elsewhere
References
1. N.H. Williams. J. Microwave Power2, 123 (1967). 2. V. Daniels. Dielectric Relaxation , Academic Press, London (1967). 3. N.E. Hill, W.E. Vaughan, A.H. Price & M. Davies. Van Nostrand Reinhold Co. London (1969). 4. J.B. Hasted. Chapman Hall (1973). 5. H. Fröhlich. Theory of Dielectrics , Oxford University Press, London (1958). 6. P. Debye. Polar Molecules , Chemical Catalog, New York (1929). 7. A. Von Hippel. Dielectric Materials and their Applications MIT Press, (1954). 8. P. Debye. Phys. Zs.36, 100 (1935). 9. J.C. Maxwell. A Treatise on Electricity and Magnetism Dover Publications, Dover (1954). 10. K.W. Wagner. Arch. Elektrotech.2, 371 (1914). 11. R.W. Sillars. J. Proc. Inst. Elect. Engrs.100, 199 (1937). 12. B.V. Hamon. Aust. J. Phys.6, 304 (1953). 13. J.S. Dryden & R.J. Meakins. Proc. Phys. Soc. B.70, 427 (1957). 14. M.M.Z. Kharadly & W. Jackson. Proc. Inst. Elect. Eng.100, 119 (1953). 15. W.H. Sutton. Am. Ceram. Soc. Bull.68, 376 (1989). 16. V. Kenkre, L. Skala, M. Weiser & J. Katz. Journal Of Materials Science26, 2483-2489 (1991). 17. G. Kriegsmann. in Journal Of Applied Physics 1960-1966, ( 1992). |
||||||||||||||||||||||||||||||||||||